式

本章では、OpenFrame PL/Iの式について説明します。

1. 概要

式は、値の表現です。式は単一の定数、変数、関数参照であるか、または定数、変数、関数参照を組み合わせたものであり、演算子と括弧を含みます。

演算子(オペレーター)が含まれた式を演算式(Operational expression)と言います。演算式に使用される定数と変数はオペランドと言います。詳細については、計算の順序を参照してください。

以下のダイアグラムは、式の文法を表したものです。

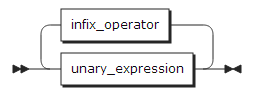
unary_expression:

elementary_expression:

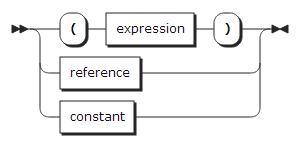
reference:

locator_qualifier:

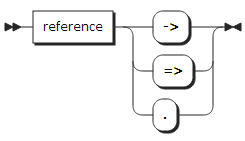
basic_reference:

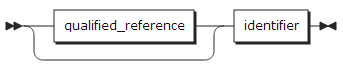
subscript_list:

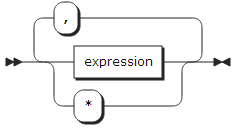
argumnet_list:

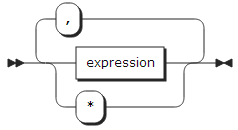
qualified_reference:

式は、スカラー式とも呼ばれる要素式と配列式、構造式に分類することができます。要素変数と配列変数は、同じ式で一緒に使用できます。

要素式(An element expression)

単一の値を表します。配列で単一のエレメントを指定する添え字付き名前、または構造体や共用体内のエレメント名を含みます。
配列式(An array expression)

値の配列を表します。次元属性を持つ構造体または共用体のメンバーを含みます。
構造式(An structure expression)

構造化された値のセットを表します。

2. 計算の順序

PL/Iステートメントには、1つ以上の式または参照が含まれています。代入ステートメントのような特別な場合を除いて、計算は任意の順序もしくは同時に行えます。

以下に例を示します。

DCL (X,Y,Z) ENTRY RETURNS(FIXED);
DCL (A,B,C) FIXED;

A = X( Y(B,C), Z(B,C) );

関数YとZは、それぞれに渡された引数の値に応じて変わってきます。したがって、Xが返す値は、先に呼び出される関数によって決まります。最初のパラメータが先に計算されると断定することはできません。状況に応じては最後のパラメータを先に計算することが適切な場合もあります。

3. ターゲット

式の計算または変換の結果はターゲットに代入されます。ターゲットは、変数、疑似変数、または中間結果のいずれかです。

変数

代入ステートメントで、ターゲットは代入記号の左側にある変数です。変数の代入は、ストリームI/O、DO、DISPLAY、レコードI/Oステートメントで行うことができます。
疑似変数

疑似変数はターゲットを表します。詳細については、組み込み関数を参照してください。
中間結果

式を計算するとき、通常ターゲット属性は、ソース、実行される演算、および2番目のオペランドの属性から部分的に派生されます。一部はデフォルトを使用したり、実装の制限と規則が存在したりします。追加演算が行われる場合、中間結果が変換されることがあります。

式を計算した後、その結果は変数または疑似変数に割り当てるために追加で変換されることがあります。このような変換はプログラマーが定義したデータの変換と同じ規則に従います。

以下に例を示します。
```
DCL A CHAR(8), B DEC FIXED(3,2), C BIN FIXED(10);
A = B + C;
```
上記の場合、式B + Cが計算され、その結果が代入される間に、4つの異なる結果が生成されます。
1. Bが2進数に変換されて割り当てられた中間結果
2. 2進数の加算結果が割り当てられた中間結果
3. 2進数の結果が10進固定小数点形式に変換されて割り当てられた中間結果
4. 10進固定小数点の値が文字形式に変換されて割り当てられた最終代入フィールドのA
  
  最初の結果の属性は、ソースBの属性、演算子、および一方のオペランドの属性によって決定されます。上記の演算で、演算子の一方のオペランドが2進数であれば、もう一方のオペランドも計算前に2進数に変換されます。2番目の結果の属性は、ソースの属性によって決定されます。3番目の結果の属性は、ソースと最終ターゲットAの属性とのつりあいによって決定されます。最終ターゲットを決定する唯一の属性はDECIMALです。

4. 演算式

演算式は、1つ以上の単一演算で構成されています。単一演算とは、演算子がオペランドの前にある接頭演算子演算または演算子が2つのオペランドの間にある挿入演算子演算のいずれかです。挿入演算子演算の2つのオペランドは、一般的に、演算の実行時には同じデータ・タイプである必要があります。PL/I式において、演算のオペランドは演算が実行される前に、必要に応じて同じタイプに変換されます。詳しい変換規則については、データ変換を参照してください。

1つの式で異なるデータ・タイプを使用することには、ほとんど制約はありませんが、様々なデータ・タイプが混在しているときは変換が行われます。実行時に変換が行われると、プログラムの実行時間が長くなります。また、変換によって精度が失われることもあります。データ・タイプが混在している式を使用する場合は、関連する変換規則についての理解が必要です。

演算の種類には、以下のようなものがあります。

4.1. 算術演算

算術演算(Arithmetic operations)は、以下の演算子のいずれかを持つオペランドの組み合わせで表すことができます。

演算子
```
＋　－　*　/　**
```

正符号と負符号は、接頭演算子または挿入演算子として使用することができます。これ以外のすべての算術演算子は、挿入演算子としてのみ使用することができます。また、算術演算はADD、SUBTRACT、DIVIDE、MULTIPLY組み込み関数を使用することも可能です。接頭演算子は挿入演算子の任意のオペランドと関連があり、その前に付けることができます。

たとえば、A/-Bでの負符号はAの値にBの-1倍の値を乗じることを示します。1つ以上の接頭演算子は単一変数と関連があり、その前に付けられます。1つ以上の正の接頭演算子(＋)を付けても累積効果はありませんが、2つの負の接頭演算子(－－)は、1つの正の接頭演算子(＋)と同じ結果になります。

算術演算の結果

式において、必要に応じてオペランドの変換が行われた後、算術演算が実行され、結果が出されます。この結果は、式の値であることも、追加的に演算が行われる場合の中間結果であることもあります。また、条件が起こることもあります。

以下の表では、様々な算術演算からの結果の属性と精度を示しています。

1つ以上のFLOATオペランドの算術演算の結果

第1オペランド(p1,q1)	第2オペランド(p2, q2)	累乗演算の結果の属性	四則演算の結果の属性	加算または減算精度	乗算精度	除算精度
FLOAT DECIMAL(p1)	FLOAT DECIMAL(p2)	FLOAT DECIMAL(p), p = MAX(p1, p2)	FLOAT DECIMAL(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FLOAT DECIMAL(p1)	FLOAT DECIMAL(p2, q2)	FLOAT DECIMAL(p), p = MAX(p1, p2)	FLOAT DECIMAL(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FIXED DECIMAL(p1,q1)	FLOAT DECIMAL(p2)	FLOAT DECIMAL(p), p = MAX(p1, p2)	FLOAT DECIMAL(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FLOAT BINARY(p1)	FLOAT BINARY(p2)	FLOAT BINARY(p), p = MAX(p1, p2)	FLOAT BINARY(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FLOAT BINARY(p1)	FIXED BINARY(p2, q2)	FLOAT BINARY(p), p = MAX(p1, p2)	FLOAT BINARY(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FIXED BINARY(p1,q1)	FLOAT BINARY(p2, q2)	FLOAT BINARY(p), p = MAX(p1, p2)	FLOAT BINARY(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FIXED BINARY(p1,q1)	FLOAT BINARY(p2)	FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)	FLOAT BINARY(p)	p = MAX( CEIL(p1*3.32), p2)	p = MAX(CEIL (p1*3.32), p2)	p = MAX(CEIL (p1*3.32), p2)
FLOAT DECIMAL(p1)	FLOAT BINARY(p2, q2)	FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)	FLOAT BINARY(p)	p = MAX( CEIL(p1*3.32), p2)	p = MAX( CEIL(p1*3.32), p2)	p = MAX(CEIL (p1*3.32), p2)
FLOAT DECIMAL(p1)	FLOAT BINARY(p2)	FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)	FLOAT BINARY(p)	p = MAX( CEIL(p1*3.32), p2)	p = MAX( CEIL(p1*3.32), p2)	p = MAX(CEIL( p1*3.32), p2)
FIXED BINARY(p1,q1)	FLOAT DECIMAL(p2)	FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))	FLOAT BINARY(p)	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))
FLOAT BINARY(p1)	FIXED DECIMAL(p2, q2)	FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))	FLOAT BINARY(p)	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))
FLOAT BINARY(p1)	FLOAT DECIMAL(p2)	FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))	FLOAT BINARY(p)	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))

第1オペランド(p1,q1)

第2オペランド(p2, q2)

累乗演算の結果の属性

四則演算の結果の属性

加算または減算精度

乗算精度

除算精度

FLOAT DECIMAL(p1)

FLOAT DECIMAL(p2)

FLOAT DECIMAL(p), p = MAX(p1, p2)

FLOAT DECIMAL(p)

p = MAX(p1, p2)

FLOAT DECIMAL(p1)

FLOAT DECIMAL(p2, q2)

FLOAT DECIMAL(p), p = MAX(p1, p2)

FLOAT DECIMAL(p)

p = MAX(p1, p2)

FIXED DECIMAL(p1,q1)

FLOAT DECIMAL(p2)

FLOAT DECIMAL(p), p = MAX(p1, p2)

FLOAT DECIMAL(p)

p = MAX(p1, p2)

FLOAT BINARY(p1)

FLOAT BINARY(p2)

FLOAT BINARY(p), p = MAX(p1, p2)

FLOAT BINARY(p)

p = MAX(p1, p2)

FLOAT BINARY(p1)

FIXED BINARY(p2, q2)

FLOAT BINARY(p), p = MAX(p1, p2)

FLOAT BINARY(p)

p = MAX(p1, p2)

FIXED BINARY(p1,q1)

FLOAT BINARY(p2, q2)

FLOAT BINARY(p), p = MAX(p1, p2)

FLOAT BINARY(p)

p = MAX(p1, p2)

FIXED BINARY(p1,q1)

FLOAT BINARY(p2)

FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)

FLOAT BINARY(p)

p = MAX( CEIL(p1*3.32), p2)

p = MAX(CEIL (p1*3.32), p2)

FLOAT DECIMAL(p1)

FLOAT BINARY(p2, q2)

FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)

FLOAT BINARY(p)

p = MAX( CEIL(p1*3.32), p2)

p = MAX(CEIL (p1*3.32), p2)

FLOAT DECIMAL(p1)

FLOAT BINARY(p2)

FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)

FLOAT BINARY(p)

p = MAX( CEIL(p1*3.32), p2)

p = MAX(CEIL( p1*3.32), p2)

FIXED BINARY(p1,q1)

FLOAT DECIMAL(p2)

FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p)

p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p1)

FIXED DECIMAL(p2, q2)

FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p)

p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p1)

FLOAT DECIMAL(p2)

FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p)

p = MAX(p1, CEIL(p2*3.32))

RULESにおける、2つのスケールのないFIXEDオペランド間の算術演算の結果

第1オペランド(p1,q1)	第2オペランド(p2, q2)	累乗演算の結果の属性	四則演算の結果の属性	加算または減算精度	乗算精度	除算精度
FIXED DECIMAL(p1,q1)	FIXED DECIMAL(p2, q2)	FLOAT DECIMAL(p), p = MAX(p1, p2)	FIXED DECIMAL(p, q)	p = 1+MAX(p1-q1, p2-q2)+q, q = MAX(q1, q2)	p = 1+p1+p2, q = q1+q2	p = N, q = N-p1+q1-q2
FIXED BINARY(p1,q1)	FIXED BINARY(p2, q2)	FLOAT BINARY(p), p = MAX(p1, p2)	FIXED BINARY(p, q)	p = 1+MAX(p1-q1, p2-q2)+q, q = MAX(q1, q2)	p = 1+p1+p2, q = q1+q2	p = M, q = M-p1+q1-q2
FIXED DECIMAL(p1,q1)	FIXED BINARY(p2, q2)	FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)	FIXED BINARY(p, q)	p = 1+MAX(r-s, p2-q2)+q, q = MAX(s, q2)	p = 1+r+p2, q = s+q2	p = M, q = M-r+s-q2
FIXED BINARY(p1,q1)	FIXED DECIMAL(p2, q2)	FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))	FIXED BINARY(p, q)	p = 1+MAX(p1-q1, t-u)+q, q = MAX(s,q1,u)	p = 1+rp1+t, q = q1+u	p = M, q = M-p1+q1-u

第1オペランド(p1,q1)

第2オペランド(p2, q2)

累乗演算の結果の属性

四則演算の結果の属性

加算または減算精度

乗算精度

除算精度

FIXED DECIMAL(p1,q1)

FIXED DECIMAL(p2, q2)

FLOAT DECIMAL(p), p = MAX(p1, p2)

FIXED DECIMAL(p, q)

p = 1+MAX(p1-q1, p2-q2)+q, q = MAX(q1, q2)

p = 1+p1+p2, q = q1+q2

p = N, q = N-p1+q1-q2

FIXED BINARY(p1,q1)

FIXED BINARY(p2, q2)

FLOAT BINARY(p), p = MAX(p1, p2)

FIXED BINARY(p, q)

p = 1+MAX(p1-q1, p2-q2)+q, q = MAX(q1, q2)

p = 1+p1+p2, q = q1+q2

p = M, q = M-p1+q1-q2

FIXED DECIMAL(p1,q1)

FIXED BINARY(p2, q2)

FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)

FIXED BINARY(p, q)

p = 1+MAX(r-s, p2-q2)+q, q = MAX(s, q2)

p = 1+r+p2, q = s+q2

p = M, q = M-r+s-q2

FIXED BINARY(p1,q1)

FIXED DECIMAL(p2, q2)

FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))

FIXED BINARY(p, q)

p = 1+MAX(p1-q1, t-u)+q, q = MAX(s,q1,u)

p = 1+rp1+t, q = q1+u

p = M, q = M-p1+q1-u

以下は、上記表の文字列の意味です。位取り係数は、-128から+127の範囲内である必要があります。

項目	説明
N	FIXED DECIMALの最大精度
M	FIXED BINARYの最大精度
r	1+CEIL(p1*3.32)
s	CEIL(ABS(q13.32))SIGN(q1)
t	1+CEIL(p2*3.32)
u	CEIL(ABS(q23.32))SIGN(q2)
r	1+CEIL(p1*3.32)

項目

説明

FIXED DECIMALの最大精度

FIXED BINARYの最大精度

1+CEIL(p1*3.32)

CEIL(ABS(q1*3.32))*SIGN(q1)

1+CEIL(p2*3.32)

CEIL(ABS(q2*3.32))*SIGN(q2)

1+CEIL(p1*3.32)

以下に例を示します。

A*B+C

まず、中間結果を出すために演算A*Bが行われます。次に、中間結果+Cという演算が実行され、式の値が得られます。PL/Iは、特定の変数から属性を得るのと同じ方式で中間結果の属性を求めます。結果の属性は、2つのオペランド(または、接頭演算の場合には単一オペランド)および関係する演算子の属性から得られます。結果の属性を求める方法については、ターゲットを参照してください。

ADD、SUBTRACT、MULTIPLY、DIVIDEなどの組み込み関数は、加算、減算、乗算、除算演算に関する精度規則を再定義することができます。FIXED除算は、オーバーフローや切り捨てが起こる場合があります。

たとえば、25+1/3を計算した結果は再定義されず、実装で定義されている最大精度の値になるため、FIXEDOVERFLOW条件が起こります。ただし、25+01/3では、定数が精度を持っているので、結果は25.3333333333333となります。

2つの計算結果は、以下の表にて確認できます。

項目	精度	結果
1 3 1/3 25 25+1/3	(1,0) (1,0) (15,14) (2,0) (15,14)	1 3 0.33333333333333 25 未定義
01 3 01/3 25 25+01/3	(2,0) (1,0) (15,13) (2,0) (15,13)	01 3 00.3333333333333 25 25.3333333333333

4.2. ビット演算

ビット演算は、以下の演算子のいずれかを持つオペランドの組み合わせで表すことができます。

演算子
```
^　　&　　|
```

NOT/排他的OR記号(^)は、接頭部または挿入演算子として使用することができます。AND(&)とOR(|)記号は、挿入演算子としてのみ使用することができます。これらの演算子は、ブール代数の場合と同じです。ビット演算のオペランドは、必要に応じて演算の実行前にビット文字列に変換されます。挿入演算のオペランドの長さが異なっている場合は、短い方に'0’Bが埋め込まれます。ビット演算の結果は、オペランドの長さと同じ長さのビット文字列になります。ビット演算はビット単位で行われます。

以下の表は、各演算子のビット位置の結果を示しています。

A	^A	B	^B	A&B	A\|B	A^B
1	0	1	0	1	1	0
1	0	0	1	0	1	1
0	1	1	0	0	1	1
0	1	0	1	0	0	0

以下の表は、ビット演算の例です。

オペランドと値	演算	結果
A = '010111’B, B = '111111’B, C = '110’B, D = 5	^A	'101000’B
^C	'001’B
A\|B	'111111’B
A^B	'101000’B
A^C	'100111’B
C&B	'110000’B
C\|B	'111111’B
A\|(^C)	'011111’B
^((^C)\|(^B))	'110111’B

オペランドと値

演算

結果

A = '010111’B,

B = '111111’B,

C = '110’B,

D = 5

'101000’B

'001’B

A|B

'111111’B

A^B

'101000’B

A^C

'100111’B

C&B

'110000’B

C|B

'111111’B

A|(^C)

'011111’B

^((^C)|(^B))

'110111’B

4.3. 比較演算

比較演算(Comparison operations)は、以下の演算子のいずれかを持つオペランドの組み合わせで表すことができます。

演算子

＜　　^＜　　＜=　　＝　　 ^＝または＜＞　　＞=　　＞　　^＞

比較演算の結果は、常に長さ1のビット文字列です。オペランドの関係が真であれば、値は'1’Bになり、偽であれば、'0’Bです。

比較は以下のとおり定義されます。

区分	説明
代数	コード化算術形式の符号付き算術値を比較します。オペランドの基数、スケール、精度、モードが異なっている場合は、算術演算変換に類似した方式で変換されます。数字データは比較される前にコード化算術形式に変換されます。＝、^＝、＜＞演算子だけが、複素数のオペランドを比較する場合に使用できます。
文字	バイトの2進数値に基づいて左から右へ文字単位で比較します。
ビット	2進数の左から右へビット単位で比較します。
グラフィック	DBCS文字を左から右へ記号単位で比較します。比較は、DBCS文字の2進数値に基づいて行われます。
ワイド文字	バイト間の2進数値に基づいて、文字を左から右へワイド文字単位で比較します。
ポインターおよびオフセット・データ	関連する演算子を含むポインターとオフセットの値を比較します。変換を行うことができるのは、オフセットからポインターへの場合だけです。

区分

説明

代数

コード化算術形式の符号付き算術値を比較します。

オペランドの基数、スケール、精度、モードが異なっている場合は、算術演算変換に類似した方式で変換されます。数字データは比較される前にコード化算術形式に変換されます。

＝、^＝、＜＞演算子だけが、複素数のオペランドを比較する場合に使用できます。

文字

バイトの2進数値に基づいて左から右へ文字単位で比較します。

ビット

2進数の左から右へビット単位で比較します。

グラフィック

DBCS文字を左から右へ記号単位で比較します。比較は、DBCS文字の2進数値に基づいて行われます。

ワイド文字

バイト間の2進数値に基づいて、文字を左から右へワイド文字単位で比較します。

ポインターおよびオフセット・データ

関連する演算子を含むポインターとオフセットの値を比較します。変換を行うことができるのは、オフセットからポインターへの場合だけです。

計算データの比較で、両オペランドのデータ・タイプが別々の比較タイプである場合には、優先度の低い方のオペランドが、もう一方のオペランドの比較タイプに合うように変換されます。

比較タイプの優先順位は以下のとおりです。

Algebraic > Widechar > Graphic > Character > Bit

たとえば、ビット文字列と固定小数点値を比較される場合、10進数値との代数比較のためにビット文字列が2進固定小数点に変換されます。また、10進数値も2進固定小数点値に変換されます。異なる長さの文字列を比較する場合は、短い方の文字列の右側に埋め込まれます。

この埋め込みは、以下のように構成されます。

文字比較では空白
ビット比較では'0’B
グラフィック比較ではグラフィック(DBCS)空白
ワイド文字比較ではワイド文字空白('0020’wx)

比較演算の例として、X＝A=Bという代入ステートメントでは、最初の等号は代入記号であり、2番目の等号は比較演算子です。したがって、AとBが等しければ、'1’B値がXに割り当てられ、等しくない場合は、'0’B値が割り当てられます。

4.4. 連結演算

連結演算(Concatenation operations)は、連結挿入演算子を持つオペランドの組み合わせです。

演算子
```
||
```

連結は、左側のオペランドの最後の文字、ビット、グラフィック、ワイド文字の直後に、右側のオペランドの最初の文字、ビット、グラフィック、ワイド文字が続く形で、オペランドの間に何もはさまずに結合されることを表します。

連結演算は、文字列(文字、ビット、グラフィック、ワイド文字)にのみ行えるので、文字タイプへの変換が行われることがあります。

4.5. 演算の組み合わせ

各種演算を同じ演算式の内で組み合わせることができます。

以下の例において、式の中の各演算は、計算の規則に従って行われますが、その前に必要なデータ変換が行われます。

 DCL RESULT BIT(3),
     A DECIMAL FIXED(1),
     B BINARY FIXED(3),
     C CHARACTER(2),
     D BIT(4);
 RESULT = A + B < C & D;

Aの10進数値が2進数に変換されます。
AとBを加算しつつ2進数加算が行われます。
2進数の結果が、変換されたCの2進数値と比較されます。
比較されたビット結果は、ビット変数Dの長さまで拡張され、&演算が行われます。
長さ4のビット文字列である&演算の結果は、変換されずに、右側で切り捨てられてRESULTに割り当てられます。

この例では、左から右に計算を行うように記述しています。計算の順序は、式に記述される演算子の優先順位によって変わります。

演算子の優先順位

式を計算する際、演算子の優先順位は以下の表を参照してください。

優先順位	演算子	演算のタイプ	備考
1	**	算術	結果はコード化算術形式です。
接頭演算子 +、-	算術	オペランドがコード化算術形式であれば、変換は不要です。ただし、オペランドが固定小数点10進数のCHARACTER文字列または数字(PICTURE)である場合は、FIXED DECIMALに変換されます。また、オペランドが浮動小数点10進数の数字(PICTURE)である場合は、FLOAT DECIMALに変換されます。オペランドがビット文字列であれば、FIXED BINARYに変換されます。
接頭演算子 ^	ビット文字列	BIT以外のデータはBITに変換されます。
2	*、/	算術	結果はコード化算術形式です。
3	挿入演算子 +、-	算術	結果はコード化算術形式です。
4	\|\|	連結	コンパイラー・オプションRULESを参照してください。
5	＜、^＜、＜=、=、^=または＜＞、＞=、＞、^＞	比較	結果は常に'1’Bあるいは'0’Bです。
6	&	ビット文字列	BIT以外のすべてのデータはBITに変換されます。
7	\|	ビット文字列	BIT以外のすべてのデータはBITに変換されます。
挿入演算子 ^	ビット文字列	BIT以外のすべてのデータはBITに変換されます。

優先順位

演算子

演算のタイプ

備考

算術

結果はコード化算術形式です。

接頭演算子 +、-

算術

オペランドがコード化算術形式であれば、変換は不要です。ただし、オペランドが固定小数点10進数のCHARACTER文字列または数字(PICTURE)である場合は、FIXED DECIMALに変換されます。

また、オペランドが浮動小数点10進数の数字(PICTURE)である場合は、FLOAT DECIMALに変換されます。オペランドがビット文字列であれば、FIXED BINARYに変換されます。

接頭演算子 ^

ビット文字列

BIT以外のデータはBITに変換されます。

*、/

算術

結果はコード化算術形式です。

挿入演算子 +、-

算術

結果はコード化算術形式です。

連結

コンパイラー・オプションRULESを参照してください。

＜、^＜、＜=、=、^=または＜＞、＞=、＞、^＞

比較

結果は常に'1’Bあるいは'0’Bです。

ビット文字列

BIT以外のすべてのデータはBITに変換されます。

ビット文字列

BIT以外のすべてのデータはBITに変換されます。

挿入演算子 ^

ビット文字列

BIT以外のすべてのデータはBITに変換されます。

演算子は、優先順位が一番高い1から一番低い7の順に並べてあります。同じ優先順位グループに属するすべての演算子は同じ優先順位を持ちます。

優先順位グループ1の場合、式の中で複数の演算子が使われると、優先順位は右から左への順になります。すなわち、最右端の指数または接頭演算子が一番高い優先順位を持ち、その次の順で優先順位を持つことになります。その他の優先順位グループは、同じ優先順位グループ内の演算子が式の中で複数使われているときは、その式の中での優先順位は左から右への順になります。

以下の式1の計算順を括弧を使って表現すると式2のようになります。

式1
```
A＋B＜C＆D
```
式2
```
(((A＋B)＜C)＆D)
```

したがって、計算順と結果は括弧の使用によって変わります。括弧内の式は、その前後にある演算子との関係を考慮する前に、1つの値として最初に計算されます。

5. 配列式

配列式は、以下のような場合に利用されます。

複数の代入または1つの代入におけるソース
ALL、ANY、SUM組み込み関数への引数
ユーザー・プロシージャと関数への引数
PUT LISTとPUT EDITステートメントのデータ・リストの項目

配列式を計算すると結果は配列になります。配列に実行されるすべての演算は行を主体としてエレメントごとに行われます。したがって、配列式で参照するすべての配列は、同じ次元の数を持つ必要があり、各次元は同じ境界を持たなければなりません。配列式は、演算子、要素変数、定数を使うことができます。演算子の組み合わせやオペランドのデータ変換の規則は、エレメント演算の場合と同じです。

5.1. 接頭演算子と配列

配列に接頭演算子の演算を行うと、同じ境界を持つ配列を生成します。

配列Aが以下のようであれば、

5　　 7　　-9
3　　-4　　 6

配列-Aは以下のようになります。

-5　　-7　　 9
-3　　 4　　-6

5.2. 挿入演算子と配列

1つのオペランドが配列変数を含む挿入演算子演算の場合、他のオペランドは別の配列やエレメントを持つことができます。

配列とエレメントの演算

エレメントと配列が挿入演算子で結ばれている計算の結果は、元の配列と同じ境界を持つ配列になります。結果の配列において各エレメントは、それぞれ対応する元の配列のエレメントと単一エレメントの結果です。

配列Aを以下のように仮定します。
```
5　　 7　　-9
3　　-4　　 6
```
配列A*2は以下のとおりです。
```
10　　14　　-18
6　　 -8　　 12
```
4＞Aの結果は、長さ1のビット文字列の配列になります。
```
0　　 0　　 1
1　　 1　　 0
```
配列エレメント演算において、エレメントは同じ配列内のエレメントになることができます。すなわち、以下のような代入ステートメントになります。

配列Aは、上記の値と同じである場合、"A＝A * A(1,1);"の結果は以下のようになります。
```
25　　 35　　-45
15　　-20　　 30
```
配列同士の演算

挿入演算子の2つのオペランドが配列である場合、その配列は次元の数が同じである必要があり、一致する次元は同じ境界(下限と上限)を持たなければなりません。演算結果は、元の配列と同じ限界を持つ配列になります。演算は、元の2つの配列の一致するエレメント間で行われます。

配列Aを以下のように仮定します。
```
5　　7　　9
3　　4　　6
```
配列Bを以下のように仮定します。
```
2　　4　　8
8　　3　　1
```
配列A＋Bは以下のとおりです。
```
7　　11　　17
11　　 7　　 7
```
配列A*Bは以下のとおりです。
```
10　　28　　72
24　　12　　 6
```
A＞Bの結果は、長さ1のビット文字列の配列になります。
```
1　　 1　　 1
0　　 1　　 1
```

6. 構造式

構造式は、構造体参照とは異なり、関連するパラメータが定数範囲を持っていると、プロシージャまたは関数の引数として使用され、代入で使用されます。構造式の中のすべての構造変数は、同じ構造である必要があります。

同じ構造という意味は以下のとおりです。

構造体は、小構造化がすべて同じで、含まれているエレメントと配列の数が同じである必要があります。
構造体内のエレメントと配列の位置は同じである必要があります。
一致する位置にある配列は同じ境界を持つ必要があります。

7. 制限付き式

制限付き式(Restricted expression)は、PL/Iに定数が必要なときに使用することができます。つまり、制限付き式は、コンパイル時に計算され、定数として使用される値の式です。

たとえば、以下のような場合に必要な定数を定義するために使用できます。

静的、パラメータ、基本宣言のエクステント
入り口宣言のエクステント
静的初期化に使用される反復因数と値

制限付き式は、一般的な式と同じですが、オペランドが以下のようなものである必要があります。

定数または名前付き定数である必要があります。名前付き定数は使用する前に宣言します。
制限付き式が適用される組み込み関数である必要があります。適用される組み込み関数については、組み込み関数を参照してください。