Expressions

This chapter describes OpenFrame PL/I expressions.

1. Overview

An expression is a representation of a value. It can be a single constant, a variable, a function reference or any combination of references with operators and parentheses.

An expression with an operator is called an operational expression. Constants and variables used in an operational expression are called operands. For more information, refer to Evaluation Order.

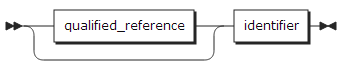
The following shows the syntax of expressions:

Syntax of Expressions

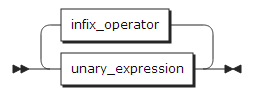
unary_expression:

elementary_expression:

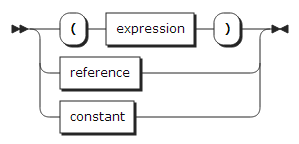
reference:

locator_qualifier:

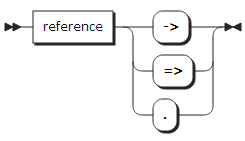
basic_reference:

subscript_list:

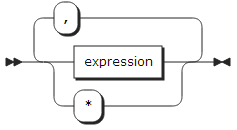
argumnet_list:

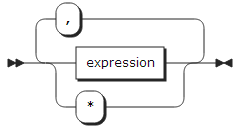
qualified_reference:

Expressions can be divided into the following element expressions, which are also called scalar expressions, array expressions, and structure expressions. An element variable and an array variable can be used together in one expression.

Element expressions

Represents a single value. This expression includes a subscripted name that specifies an element of an array or an elementary name in a structure or set.
Array expressions

Represents an array of values. This expression includes the member of a structure or set that has a dimension attribute.
Structure expressions

Represents a structured set of values.

2. Evaluation Order

A PL/I statement includes one or more expressions or references. They can be evaluated in any order or at the same time except for special cases like an assignment statement.

The following is an example:

DCL (X,Y,Z) ENTRY RETURNS(FIXED);
DCL (A,B,C) FIXED;

A = X( Y(B,C), Z(B,C) );

The Y and Z functions can change argument values. Therefore, a value returned by X can be different according to the function that is called first. In some cases, it is more appropriate that the last is calculated first.

3. Targets

The result of an expression evaluation or a conversion is assigned to a target. Targets can be variables, pseudo variables, or intermediate results.

Variables

In an assignment statement, a target is a variable to the left of an assignment symbol. Assignments to variables can occur in stream I/O, DO, DISPLAY, or record I/O statements.
Pseudo variables

Represents a target field. For more information, refer to Built-in Functions.
Intermediate results

When an expression is evaluated, the target attributes are determined depending on the source attributes, attributes of the operation to be executed, or attributes of a second operand. Some defaults can be used, and some implementation restrictions and conventions exist. When additional operation is executed, an intermediate result can be converted.

The result of an expression evaluation can be converted to be assigned to a variable or pseudo variable. The conversions must follow programmer-defined rules such as a data conversion rule.

The following is an example:
```
DCL A CHAR(8), B DEC FIXED(3,2), C BIN FIXED(10);
A = B + C;
```
The expression B + C is evaluated. While the result is assigned to A, the following four different results will be generated:
1. Intermediate result to which the converted binary, which is equivalent of B, is assigned
2. Intermediate result to which the binary result of the addition is assigned
3. Intermediate result to which the converted decimal fixed-point, which is equivalent of the previous intermediate result, is assigned
4. A, the final result to which the converted character, which is equivalent of the previous intermediate result, is assigned
The attributes of the first result are determined by the attributes of the source B, the operator, and the attributes of the other operand. If one operand in an arithmetic expression is binary, the other operand will be converted to binary before the evaluation. The attributes of the second result are determined by the source attributes. The attributes of the third result are determined partially by the source attributes and partially by the attributes of the final target A. The only attribute determined by the final target is DECIMAL.

4. Operational Expressions

Operational expressions consists of one or more operations. A single operation is either a prefix operation (an operator comes before an operand) or an infix operation (an operator comes between two operands). In general, two operands of an infix operation must have the same data type when the evaluation is executed. If necessary, operands of an operation are converted so that they have the same data type before an operation execution. For information about the conversion rule, refer to Data Conversion.

There are some restrictions on the use of different data types in an expression. Using different data types requires a conversion. If a conversion is executed at run time, it will take longer to run the program. Conversion also decreases precision.

Operations can be divided into arithmetic, bit, comparison, and concatenation operations.

4.1. Arithmetic Operations

An arithmetic operation is a combination of operands and one of the following operators:

Operators
```
+　-　*　/　**
```

The plus and minus signs can be used as a both prefix and infix operator. The other signs can only be used as infix operators. An arithmetic operation can be specified using the built-in ADD, SUBTRACT, DIVIDE, and MULTIPLY functions. A prefix operator can precede and be associated with any operand of an infix operation. For example, the minus sign in A/-B means that the value of A is divided by -1 times the value of B. Multiple prefix operators can precede and be associated with a single variable. Multiple positive prefix operators have no cumulative effect, but two negative prefix operators have the same effect as a single positive prefix operator.

Results of Arithmetic Operations

If necessary, an arithmetic operation will be executed after operands have been converted, and a result will be obtained. A condition can occur, or the result can be an expression value or an intermediate result for an additional operation.

The following tables show attributes and precisions for various results of arithmetic operations:

Results of arithmetic operations for one or more FLOAT operands

1st Operand (p1,q1)	2nd Operand (p2, q2)	Attributes of an Exponentiation Result	Attributes of a Four Fundamental Arithmetic Operation Result	Addition or Subtraction Precision	Multiplication Precision	Division Precision
FLOAT DECIMAL(p1)	FLOAT DECIMAL(p2)	FLOAT DECIMAL(p), p = MAX(p1, p2)	FLOAT DECIMAL(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FLOAT DECIMAL(p1)	FLOAT DECIMAL(p2, q2)	FLOAT DECIMAL(p), p = MAX(p1, p2)	FLOAT DECIMAL(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FIXED DECIMAL(p1,q1)	FLOAT DECIMAL(p2)	FLOAT DECIMAL(p), p = MAX(p1, p2)	FLOAT DECIMAL(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FLOAT BINARY(p1)	FLOAT BINARY(p2)	FLOAT BINARY(p), p = MAX(p1, p2)	FLOAT BINARY(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FLOAT BINARY(p1)	FIXED BINARY(p2, q2)	FLOAT BINARY(p), p = MAX(p1, p2)	FLOAT BINARY(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FIXED BINARY(p1,q1)	FLOAT BINARY(p2, q2)	FLOAT BINARY(p), p = MAX(p1, p2)	FLOAT BINARY(p)	p = MAX(p1, p2)	p = MAX(p1, p2)	p = MAX(p1, p2)
FIXED BINARY(p1,q1)	FLOAT BINARY(p2)	FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)	FLOAT BINARY(p)	p = MAX( CEIL(p1*3.32), p2)	p = MAX(CEIL (p1*3.32), p2)	p = MAX(CEIL (p1*3.32), p2)
FLOAT DECIMAL(p1)	FLOAT BINARY(p2, q2)	FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)	FLOAT BINARY(p)	p = MAX( CEIL(p1*3.32), p2)	p = MAX( CEIL(p1*3.32), p2)	p = MAX(CEIL (p1*3.32), p2)
FLOAT DECIMAL(p1)	FLOAT BINARY(p2)	FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)	FLOAT BINARY(p)	p = MAX( CEIL(p1*3.32), p2)	p = MAX( CEIL(p1*3.32), p2)	p = MAX(CEIL( p1*3.32), p2)
FIXED BINARY(p1,q1)	FLOAT DECIMAL(p2)	FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))	FLOAT BINARY(p)	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))
FLOAT BINARY(p1)	FIXED DECIMAL(p2, q2)	FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))	FLOAT BINARY(p)	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))
FLOAT BINARY(p1)	FLOAT DECIMAL(p2)	FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))	FLOAT BINARY(p)	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))	p = MAX(p1, CEIL(p2*3.32))

1st Operand (p1,q1)

2nd Operand (p2, q2)

Attributes of an Exponentiation Result

Attributes of a Four Fundamental Arithmetic Operation Result

Addition or Subtraction Precision

Multiplication Precision

Division Precision

FLOAT DECIMAL(p1)

FLOAT DECIMAL(p2)

FLOAT DECIMAL(p), p = MAX(p1, p2)

FLOAT DECIMAL(p)

p = MAX(p1, p2)

FLOAT DECIMAL(p1)

FLOAT DECIMAL(p2, q2)

FLOAT DECIMAL(p), p = MAX(p1, p2)

FLOAT DECIMAL(p)

p = MAX(p1, p2)

FIXED DECIMAL(p1,q1)

FLOAT DECIMAL(p2)

FLOAT DECIMAL(p), p = MAX(p1, p2)

FLOAT DECIMAL(p)

p = MAX(p1, p2)

FLOAT BINARY(p1)

FLOAT BINARY(p2)

FLOAT BINARY(p), p = MAX(p1, p2)

FLOAT BINARY(p)

p = MAX(p1, p2)

FLOAT BINARY(p1)

FIXED BINARY(p2, q2)

FLOAT BINARY(p), p = MAX(p1, p2)

FLOAT BINARY(p)

p = MAX(p1, p2)

FIXED BINARY(p1,q1)

FLOAT BINARY(p2, q2)

FLOAT BINARY(p), p = MAX(p1, p2)

FLOAT BINARY(p)

p = MAX(p1, p2)

FIXED BINARY(p1,q1)

FLOAT BINARY(p2)

FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)

FLOAT BINARY(p)

p = MAX( CEIL(p1*3.32), p2)

p = MAX(CEIL (p1*3.32), p2)

FLOAT DECIMAL(p1)

FLOAT BINARY(p2, q2)

FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)

FLOAT BINARY(p)

p = MAX( CEIL(p1*3.32), p2)

p = MAX(CEIL (p1*3.32), p2)

FLOAT DECIMAL(p1)

FLOAT BINARY(p2)

FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)

FLOAT BINARY(p)

p = MAX( CEIL(p1*3.32), p2)

p = MAX(CEIL( p1*3.32), p2)

FIXED BINARY(p1,q1)

FLOAT DECIMAL(p2)

FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p)

p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p1)

FIXED DECIMAL(p2, q2)

FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p)

p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p1)

FLOAT DECIMAL(p2)

FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))

FLOAT BINARY(p)

p = MAX(p1, CEIL(p2*3.32))

Results of arithmetic operations between two FIXED operands under RULES

1st Operand (p1,q1)	2nd Operand (p2, q2)	Attributes of an Exponentiation Result	Attributes of a Four Fundamental Arithmetic Operation Result	Addition or Subtraction Precision	Multiplication Precision	Division Precision
FIXED DECIMAL(p1,q1)	FIXED DECIMAL(p2, q2)	FLOAT DECIMAL(p), p = MAX(p1, p2)	FIXED DECIMAL(p, q)	p = 1+MAX(p1-q1, p2-q2)+q, q = MAX(q1, q2)	p = 1+p1+p2, q = q1+q2	p = N, q = N-p1+q1-q2
FIXED BINARY(p1,q1)	FIXED BINARY(p2, q2)	FLOAT BINARY(p), p = MAX(p1, p2)	FIXED BINARY(p, q)	p = 1+MAX(p1-q1, p2-q2)+q, q = MAX(q1, q2)	p = 1+p1+p2, q = q1+q2	p = M, q = M-p1+q1-q2
FIXED DECIMAL(p1,q1)	FIXED BINARY(p2, q2)	FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)	FIXED BINARY(p, q)	p = 1+MAX(r-s, p2-q2)+q, q = MAX(s, q2)	p = 1+r+p2, q = s+q2	p = M, q = M-r+s-q2
FIXED BINARY(p1,q1)	FIXED DECIMAL(p2, q2)	FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))	FIXED BINARY(p, q)	p = 1+MAX(p1-q1, t-u)+q, q = MAX(s,q1,u)	p = 1+rp1+t, q = q1+u	p = M, q = M-p1+q1-u

1st Operand (p1,q1)

2nd Operand (p2, q2)

Attributes of an Exponentiation Result

Attributes of a Four Fundamental Arithmetic Operation Result

Addition or Subtraction Precision

Multiplication Precision

Division Precision

FIXED DECIMAL(p1,q1)

FIXED DECIMAL(p2, q2)

FLOAT DECIMAL(p), p = MAX(p1, p2)

FIXED DECIMAL(p, q)

p = 1+MAX(p1-q1, p2-q2)+q, q = MAX(q1, q2)

p = 1+p1+p2, q = q1+q2

p = N, q = N-p1+q1-q2

FIXED BINARY(p1,q1)

FIXED BINARY(p2, q2)

FLOAT BINARY(p), p = MAX(p1, p2)

FIXED BINARY(p, q)

p = 1+MAX(p1-q1, p2-q2)+q, q = MAX(q1, q2)

p = 1+p1+p2, q = q1+q2

p = M, q = M-p1+q1-q2

FIXED DECIMAL(p1,q1)

FIXED BINARY(p2, q2)

FLOAT BINARY(p), p = MAX( CEIL(p1*3.32), p2)

FIXED BINARY(p, q)

p = 1+MAX(r-s, p2-q2)+q, q = MAX(s, q2)

p = 1+r+p2, q = s+q2

p = M, q = M-r+s-q2

FIXED BINARY(p1,q1)

FIXED DECIMAL(p2, q2)

FLOAT BINARY(p), p = MAX(p1, CEIL(p2*3.32))

FIXED BINARY(p, q)

p = 1+MAX(p1-q1,

t-u)+q, q = MAX(s,q1,u)

p = 1+rp1+t, q = q1+u

p = M, q = M-p1+q1-u

The following table describes each character used in the above tables. The scaling factor must be between -128 and +127.

Item	Description
N	Maximum precision of FIXED DECIMAL
M	Maximum precision of FIXED BINARY
r	1+CEIL(p1*3.32)
s	CEIL(ABS(q13.32))SIGN(q1)
t	1+CEIL(p2*3.32)
u	CEIL(ABS(q23.32))SIGN(q2)
r	1+CEIL(p1*3.32)

Item

Description

Maximum precision of FIXED DECIMAL

Maximum precision of FIXED BINARY

1+CEIL(p1*3.32)

CEIL(ABS(q1*3.32))*SIGN(q1)

1+CEIL(p2*3.32)

CEIL(ABS(q2*3.32))*SIGN(q2)

1+CEIL(p1*3.32)

Let’s look at the following expression example.

A*B+C

In the example, the operation A*B is executed first to get an intermediate result. The expression value is then obtained by executing the intermediate result + C.

The method for getting attributes of an intermediate result is the same as that of a variable. Result attributes can be determined by attributes of two operands (or one operand in the case of a prefix operation) and a operator. For more information about how to get result attributes, refer to Targets.

The built-in ADD, SUBTRACT, MULTIPLY, and DIVIDE functions enable the redefinition of the implementation of precision rules for addition, subtraction, multiplication, and division operations.

A FIXED division can cause an overflow or truncation. For example, the result of 25+1/3 is undefined, so the FIXEDOVERFLOW condition will occur because a division result defines a precision within a maximum implementation value. However, the result of 25+01/3 is 25.3333333333333 if the maximum precision is 15 because constants have a precision.

The following table shows the results of the two evaluations:

Item	Precision	Result
1 3 1/3 25 25+1/3	(1,0) (1,0) (15,14) (2,0) (15,14)	1 3 0.33333333333333 25 Undefined
01 3 01/3 25 25+01/3	(2,0) (1,0) (15,13) (2,0) (15,13)	01 3 00.3333333333333 25 25.3333333333333

4.2. Bit Operations

A bit operation is a combination of operands and one of the following operators:

Operators
```
^　　&　　|
```

The not/exclusive-or symbol (^) cannot be used as a prefix or infix operator. The and (&) and or symbols (|) can only be used as infix operators and have the same functionality as they would in Boolean algebra. Operands of a bit operation are converted to a bit string if necessary before the operation execution. If the operands have different lengths, a shorter operand will be padded on the right side with a value of '0’B. The result of a bit operation is a bit string with the same length of operands. A bit operation is executed in bit units.

The following table shows the results of each bit position for each operator:

A	^A	B	^B	A&B	A\|B	A^B
1	0	1	0	1	1	0
1	0	0	1	0	1	1
0	1	1	0	0	1	1
0	1	0	1	0	0	0

The following table shows examples of bit operations:

Operands and Values	Operation	Result
A = '010111’B, B = '111111’B, C = '110’B, D = 5	^A	'101000’B
^C	'001’B
A\|B	'111111’B
A^B	'101000’B
A^C	'100111’B
C&B	'110000’B
C\|B	'111111’B
A\|(^C)	'011111’B
^((^C)\|(^B))	'110111’B

Operands and Values

Operation

Result

A = '010111’B,

B = '111111’B,

C = '110’B,

D = 5

'101000’B

'001’B

A|B

'111111’B

A^B

'101000’B

A^C

'100111’B

C&B

'110000’B

C|B

'111111’B

A|(^C)

'011111’B

^((^C)|(^B))

'110111’B

4.3. Comparison Operations

A comparison operation is a combination of operands and one of the following operators:

Operators

<　　^<　　<=　　=　 ^= or <>　　>=　　>　　^>

The result of a comparison operation is always a bit string with the length of 1. If the comparison result is true, the resulting value will be '1’B. Otherwise, it will be '0’B.

Comparisons are defined as follows:

Classification	Description
Algebraic	Signed arithmetic vales in a coded arithmetic form are compared. If operands have different bases, scales, precisions, or modes, they will be converted using a similar method to that used for arithmetic operation conversions. Numeric character data is converted to coded arithmetic data before comparison. Only the ＝, ^＝, and＜＞operators can be used to compare operands that are complex numbers.
Character	Characters are compared left-to-right in a character unit according to the binary value of the bytes.
Bit	Binary digits are compared left-to-right in bit units.
Graphic	DBCS characters are compared left-to-right order in a symbol unit. The comparison is based on the binary values of DBCS characters.
Widechar	Characters are compared left-to-right in a symbol unit according to the binary value of byte-pairs.
Pointer and offset data	Pointer and offset values that include relational operators are compared. The only conversion that can occur is offset to pointer.

Classification

Description

Algebraic

Signed arithmetic vales in a coded arithmetic form are compared.

If operands have different bases, scales, precisions, or modes, they will be converted using a similar method to that used for arithmetic operation conversions. Numeric character data is converted to coded arithmetic data before comparison.

Only the ＝, ^＝, and＜＞operators can be used to compare operands that are complex numbers.

Character

Characters are compared left-to-right in a character unit according to the binary value of the bytes.

Bit

Binary digits are compared left-to-right in bit units.

Graphic

DBCS characters are compared left-to-right order in a symbol unit. The comparison is based on the binary values of DBCS characters.

Widechar

Characters are compared left-to-right in a symbol unit according to the binary value of byte-pairs.

Pointer and offset data

Pointer and offset values that include relational operators are compared. The only conversion that can occur is offset to pointer.

If operands of a computational data comparison has data types that are appropriate to a different comparison type, an operand with a lower priority will be converted to be appropriate to the comparison type of another operand.

The priority order of comparison types is as follows:

Algebraic > Widechar > Graphic > Character > Bit

For example, if a bit string is compared with a FIXED DECIMAL value, the bit string will be converted to a FIXED BINARY for algebraic comparison with the DECIMAL value. The DECIMAL value will also be converted to FIXED BINARY. If strings with different lengths are compared, the shorter string will be padded on the right side.

The padding is as follows:

Blanks for a character comparison
'0’B for a bit comparison
A graphic (DBCS) blank for a graphic comparison
A widechar blank ('0020’wx) for a widechar comparison

In the example of X＝A=B, the first equal symbol is the assignment symbol, and the second equal symbol is the comparison operator. Therefore, if A is equal to B, '1’B is assigned to X. Otherwise, '0’B is assigned.

4.4. Concatenation Operations

A concatenation operation is a combination of operands and the concatenation infix operator.

Operator
```
||
```

Concatenation means the last character, bit, graphic, or widechar of an operand is combined with the first character, bit, graphic, or widechar of the other operand without anything between them.

Since concatenation operations can only be executed for strings (character, bit, graphic, and widechar), conversion to a string type can occur.

4.5. Combinations of Operations

Different types of operations can be combined in an operational expression.

The following is an example. Each operation in the expression is executed according to the rules for the operation type. Necessary data conversion can occur before executing the operation.

 DCL RESULT BIT(3),
     A DECIMAL FIXED(1),
     B BINARY FIXED(3),
     C CHARACTER(2),
     D BIT(4);
 RESULT = A + B < C & D;

The decimal value of A is converted to binary.
The binary addition (A + B) is executed.
The binary result is compared with the converted binary value of C.
The bit comparison result is extended to the length of the bit variable D, and the & operation is executed.
The bit string result of the & operation with the length of 4 is not converted but truncated on the right. It is assigned to RESULT.

The above example is executed left-to-right between the order of operations. The execution order depends on the priorities of operators in the expression.

Priority of Operators

The following table shows the priority of operations in expressions:

Priority	Operator	Operation Type	Remarks
1	**	Arithmetic	Result is coded arithmetic.
	prefix +,-	Arithmetic	If an operand is coded arithmetic, a conversion is not necessary. If an operand is a CHARACTER string or a numeric character (PICTURE) representation of a fixed-point decimal number, it will be converted to a FIXED DECIMAL. If an operand is a numeric character (PICTURE) representation of a floating-point decimal number, it will be converted to a FLOAT DECIMAL. If an operand is a BIT string, it will be converted to a FIXED BINARY.
	prefix ^	Bit string	All non-BIT data is converted to BIT.
2	*, /	Arithmetic	A result has a coded arithmetic type.
3	infix +.-	Arithmetic	A result has a coded arithmetic type.
4	\|\|	Concatenation	Refers to compiler option rules.
5	<, ^<, <=, =, ^= or <>, >=, >, ^>	Comparison	A result is always either '1’B or '0’B.
6	&	Bit string	All non-BIT data is converted to BIT.
7	\|	Bit string	All non-BIT data is converted to BIT.
	infix ^	Bit string	All non-BIT data is converted to BIT.

Priority

Operator

Operation Type

Remarks

Arithmetic

Result is coded arithmetic.

prefix +,-

Arithmetic

If an operand is coded arithmetic, a conversion is not necessary. If an operand is a CHARACTER string or a numeric character (PICTURE) representation of a fixed-point decimal number, it will be converted to a FIXED DECIMAL. If an operand is a numeric character (PICTURE) representation of a floating-point decimal number, it will be converted to a FLOAT DECIMAL. If an operand is a BIT string, it will be converted to a FIXED BINARY.

prefix ^

Bit string

All non-BIT data is converted to BIT.

*, /

Arithmetic

A result has a coded arithmetic type.

infix +.-

Arithmetic

A result has a coded arithmetic type.

Concatenation

Refers to compiler option rules.

<, ^<, <=, =, ^= or <>, >=, >, ^>

Comparison

A result is always either '1’B or '0’B.

Bit string

All non-BIT data is converted to BIT.

Bit string

All non-BIT data is converted to BIT.

infix ^

Bit string

All non-BIT data is converted to BIT.

In the above table, operators in the same priority group have the same priority.

If multiple operators that are included in the priority group 1 are used in an expression, the priority order is right-to-left. That is, the rightmost exponentiation or prefix operator has the highest priority, the next rightmost operator has the next highest priority, and so on. If multiple operators that are included in another priority group in an expression, the priority order is left-to-right.

The following expression 1 is the same as the expression 2 when using parentheses to express priorities.

Expression 1
```
A＋B＜C＆D
```
Expression 2
```
(((A＋B)＜C)＆D)
```

The evaluation order and result change according to the use of parentheses. Expressions embedded with parentheses are evaluated to a single value before relationship with other operators is considered.

5. Array Expressions

Array expressions are used as the following:

Sources in one or multiple assignments
Arguments of ALL, ANY, and SUM built-in functions
Arguments of user procedures and functions
Items in a data list of a PUT LIST and PUT EDIT statements

The result of an array expression is an array. All operations are executed for each element in a row order. Therefore, all arrays in an array expression must have the same number of dimensions and each dimension must have the same bounds.

Array expressions can include operators, element variables, and constants. The rules for combining operators and converting operand data are the same as those for element operations.

5.1. Prefix Operators and Arrays

The result of an operation of a prefix operator in an array is an array that has the same bounds as a source array.

If the array A is as follows:

5　　 7　　-9
3　　-4　　 6

then -A will be as follows:

-5　　-7　　 9
-3　　 4　　-6

5.2. Infix Operators and Arrays

Infix operations that include an array variable as an operand can have another array as the other operand or an element.

Array-and-element operations

The result of an expression with an element, array, or infix operator is an array that has the same bounds as a source array. In a result array, each element is the result of the operation between a single element and the source array’s corresponding element.

If the array A is as follows:
```
5　　 7　　-9
3　　-4　　 6
```
then A*2 is as follows:
```
10　　14　　-18
6　　 -8　　 12
```
and the result of 4＞A is an array of bit strings with lengths of 1.
```
0　　 0　　 1
1　　 1　　 0
```
In array-and-element operations, an element can be an element of the same array.

If the array A is the same as the above example, the result of the assignment statement "A＝A * A(1,1);" will be as follows:
```
25　　 35　　-45
15　　-20　　 30
```
Array-and-array operations

If two operands of an infix operator are arrays, the arrays must have the same number of dimensions. Corresponding dimensions must have the same lower and upper bounds. The result is an array with the same bounds as a source array. Operations are executed on corresponding elements of two source arrays.

If the array A is as follows:
```
5　　7　　9
3　　4　　6
```
and the array B is as follows:
```
2　　4　　8
8　　3　　1
```
then the result of A＋B will be:
```
7　　11　　17
11　　 7　　 7
```
the result of A*B will be:
```
10　　28　　72
24　　12　　 6
```
and the result of A＞B will be an array of bit strings with lengths of 1.
```
1　　 1　　 1
0　　 1　　 1
```

6. Structure Expressions

Structure expressions, unlike structure references, are used in assignments as arguments of procedures or functions if related parameter has constant extents. All structure variables in a structure expression must have the same structure.

Same structure means the following:

Structures must have the same sub-structures and the same number of included elements and arrays.
Positions of elements and arrays in structures must be the same.
Arrays in corresponding positions must have the same bounds.

7. Restricted Expressions

Restricted expressions can be used when a PL/I requires a constant. In other words, a restricted expression is an expression of a value used as a constant after being evaluated during compilation.

For example, restricted expressions can be used to define constants required for the following cases:

Extents in static, parameter, and based declarations
Extents in entry descriptions
Iteration factors and values used in static initialization

Restricted expressions are the same as general expressions, but have the following restrictions for operands:

Must be a constant or a named constant. A named constant must be declared before use.
Must be a built-in function to which a restricted expression can be applied. For more information about built-in functions, refer to Built-in Functions.